Prefill vs Decode

Two major operations in modern LLM inference

Two major operations in modern LLM inference are prefill and decode. It’s important to know what they are and how they differ. Most modern LLMs are variations of GPT, which is Decoder-only model. These models take an input (or prompt), process it, sample the next token, and use the previous input + sampled token as the next input in an autoregressive manner. This is called “decoding” and occurs token-by-token.

What is Prefill?

Prefill happens when the input or prompt are given to the model. This is done by computing all tokens in parallel, just like we do in Transformer’s Encoder Layer. Unlike BERT or T5, which allows bidirectional attention, standard Decoder-only models like GPT need to apply causal masking. This is because the model is trained this way — to avoid “cheating” the next token which may lead to lack of next token prediction ability.

Prefill is known to be compute-bound, because it uses Matrix-Matrix Multiplication(GEMM), which processes self-attention to each and every token in the given prompt in parallel. GEMM has high arithmetic intensity which is a perfect task for GPUs.

Ignoring minor calculations such as splitting/concatenating heads for Multi-Head Attention, the major operations in a single Transformer block are: 1) project each token to Q, K, V, 2) calculate attention ($\text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V$), and 3) pass through the FFN. In the Prefill stage, we do all of these for every token in parallel, with causal mask applied.

Each token’s KV values are stored into a memory space called KV Cache, and reused throughout the decode process. We will look through what KV Cache is later in this post.

What is Decode?

As mentioned above, decode happens when we concatenate the sampled next token to the original prompt and use it as the next input of the model. Decoding ends when it samples <eos> (special token indicating end of a sequence) or reaches the maximum length — either specified by the user or the LLM.

Someone may ask, why does Decode differ from Prefill if both of them are essentially inserting input to a Decoder model and processing it? This would be true if we didn’t use KV Cache.

KV Cache is a mechanism to store key-value tensors in GPU memory(VRAM) to avoid redundant computation. If we can save the KV values during the decoding process, we can just reuse the KV values and only calculate the QKV for the last sampled token.

If it weren’t for KV cache, decoding would be same as “prefilling with the next token added” which is very inefficient since we need to recalculate all the tokens from start. Image provided from Sebastian Raschka clearly visualizes this inefficient computation if we didn’t use KV cache: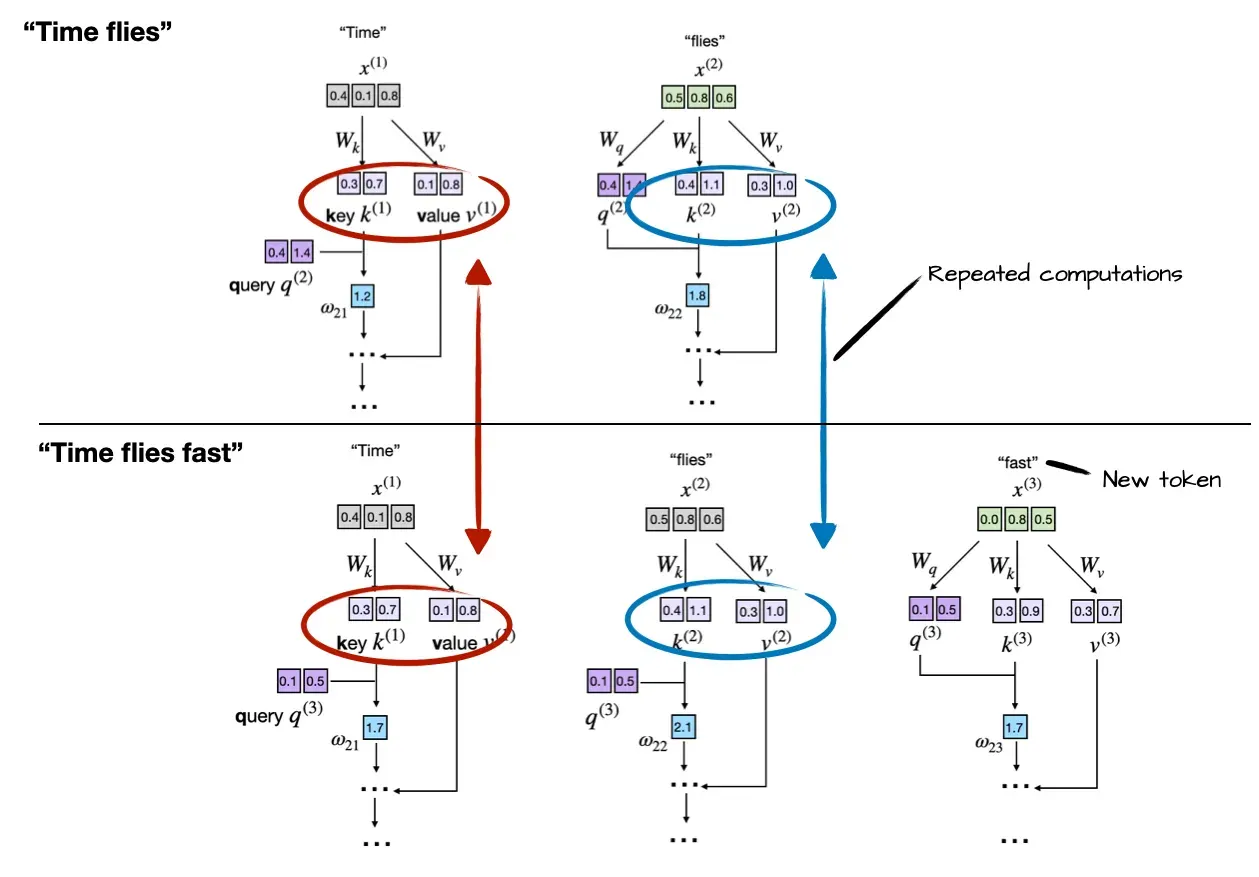
Image from Understanding and Coding the KV Cache in LLMs from Scratch by Sebastian Raschka

During decode, we calculate attention in Matrix-Vector Multiplication(GEMV). Unlike Prefill, we only need to matrix multiply the new token’s Q value(vector) with the previous KV values(matrix). Therefore the only values calculated are current token’s Q,K,V values.

As you may notice, using KV cache is a tradeoff of computation and memory/latency. While we only need to calculate KV for the last sampled token, we do need to load all the previous token’s KVs from KV Cache. This is why Decoding process (with KV Cache) is memory-bound or bandwidth limited. Note that while decoding process is computationally more efficient, it may be slower depending on the latency loading the KV cache.

Example

We are going to see how Prefill and Decode works in one example, with the unfinished sequence “The cat sat”.

Let’s say the prompt given to the model is “The cat sat”.

First, we don’t have any pre-calculated KV Cache of these tokens so we would need to “prefill” them(<sos> here means “start of sequence” which is used as a special token indicating the sequence starts).

We need to forward pass the QKV in order to calculate the attention score, and since we know all the tokens, we can use causal masking to calculate attention scores using each token’s Q in a parallel manner. As mentioned above Prefill stage is compute-bound because we need to calculate all the attention scores for each token’s Q, which is computationally heavy.

The image below represents a single head during the attention calculation($QK^T$) with softmax applied.

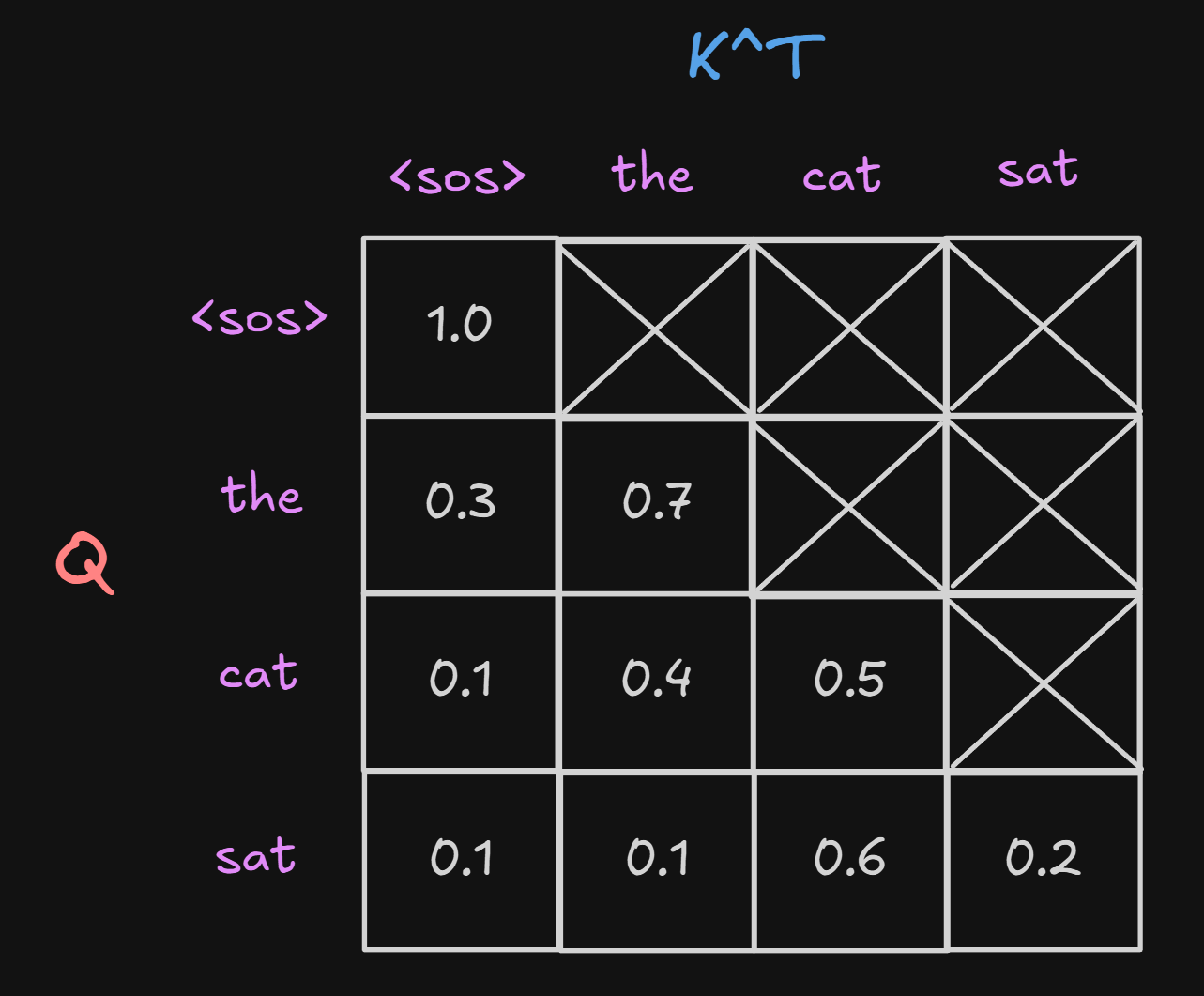
As you can see, the Query cannot see the tokens further(in the future) than itself because causal masking is applied. Also note that I colored the tokens that need to be calculated(or forward passed) in pink and tokens that already have KV cache in memory in white. Since we don’t have any memory of the prompt in Prefill stage, it’s normal to see all tokens need QKV values calculated. Each token’s KV values are saved in KV Cache since the sequence didn’t end yet.

After the forward pass of the model, we can sample the next new token, which may be “on”.

Now, since the model finished processing the prompt, it takes the original input(or prompt) including the sampled token from the previous step.

Now let’s look at how Attention calculation in Decoding Stage is different from Prefill Stage.

There are two major differences here.
First, it’s not a n_seq x n_seq matrix, but instead it’s a vector. This is because in order to sample the next token, we only need the attention scores between the sampled token’s Q and all previous K values(This is also the reason why we don’t need to save previous token’s Q values!).
Second, as I’ve mentioned above, the tokens written in white don’t need calculation. This is because we already saved the token’s KV values in KV Cache. We load and use them instead of recalculating it. This saves computation time. Since we use the previous token(<sos>, the, cat, sat)’s KV Cache, we only need to forward pass QKV for the new token “on”.

The decoding process will keep iterating until it exceeds the maximum sequence size or after it reaches the <eos> token (e.g., <sos>, the, cat, sat, on, the, mat, <eos>).

What are Inference Engines (e.g., vLLM or SGLang) trying to do?

LLM Inference Engines are getting lots of traction due to the high computational cost of LLM model’s autoregressive behavior.

Developers and Researchers realized that the bottleneck of Inference may come from memory more than computation. This is because luckily modern GPU(and CUDA software) is optimized to calculate major operations such as matrix multiplication, while loading KV Cache for attention calculation, without any inference optimization, may work slow, leading to huge latency.

In the PagedAttention paper, it is stated as:

Additionally, given the current trends, the GPU’s computation speed grows faster than the memory capacity. For example, from NVIDIA A100 to H100, The FLOPS increases by more than 2x, but the GPU memory stays at 80GB maximum. Therefore, we believe the memory will become an increasingly significant bottleneck.

PagedAttention addresses this by managing KV cache memory in non-contiguous blocks, similar to OS virtual memory—a topic I’ll explore in a future post.

Conclusion

Through this post, we decomposed LLM inference into its two core phases: the compute-bound Prefill and the memory-bound Decode. Understanding this distinction is crucial to appreciating the architecture of modern serving systems. While I only scratched the surface of inference optimization here, this concept is the key to unlocking high-throughput serving.

This post sets the foundation for my upcoming deep dives into AI Systems. I look forward to sharing more in-depth analyses, specifically focusing on vLLM and memory optimization in the near term. Thank you for reading!